Mesure de la courbe de transmission d’un filtre H-alpha

Dans cet article, nous allons mesurer la courbe de transmission d’un filtre Hα à l’aide d’un spectroscope. La transmission d’un filtre, utilisé en visuel ou en astrophotographie, est une caractéristique essentielle qui informe l’utilisateur de la bande passante du filtre, c’est-à-dire la plage de longueurs d’onde que le filtre laisse passer et de l’efficacité avec laquelle ces longueurs d’onde sont transmises (un filtre n’a jamais une transmission de 100 %). Dans une première partie, quelques rappels de spectroscopie seront faits puis le dispositif de mesure sera décrit et enfin la courbe de transmission sera présentée.

I. Quelques rappels de spectroscopie

Un spectre représente la décomposition de la lumière émise par une source suivant les différentes longueurs d’onde qui la composent. La spectroscopie consiste à obtenir, à l’aide d’un dispositif particulier, et analyser le spectre d’une source afin d’en déduire des propriétés physiques. Il existe différents types de spectres : spectre continu, spectre d’émission et spectre d’absorption. Ceux-ci sont représentés sur la figure 1. Un spectre continu est émis par tout corps chauffé. Comme son nom l’indique, l’intensité lumineuse est répartie de manière continue sur toute la gamme en longueur d’onde.

A l’inverse, les spectres d’émission et d’absorption sont des spectres de raies car il y a des émissions ou des absorptions uniquement à des longueurs d’onde bien précises. Les spectres d’émission et d’absorption sont produits lors de transitions électroniques ayant lieu dans un atome. Il y a émission lorsque un électron passe d’un niveau d’énergie vers un autre d’énergie plus basse. L’absorption est le phénomène inverse, si bien que les deux spectres sont complémentaires. Les spectres d’émission et d’absorption sont caractéristiques d’un élément chimique donné. Un tel spectre est la « carte d’identité » d’un élément chimique.

II. Dispositif expérimental

Le dispositif expérimental utilisé pour cette mesure est présenté sur la figure 2.

Il se compose de :

• Un module d’étalonnage Alpy contenant une lampe ArNe pour l’étalonnage et une lampe blanche utilisée pour faire des flats.
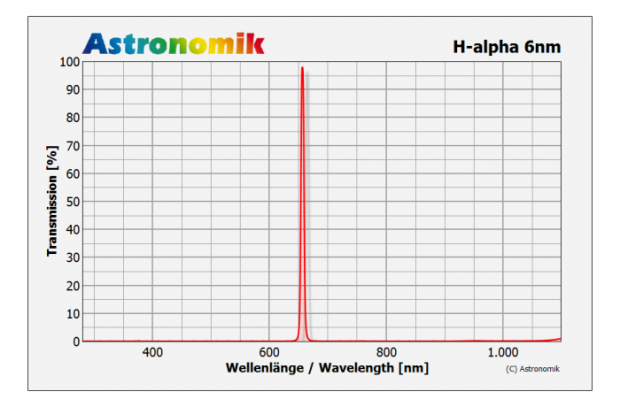
• Une roue à filtre dans laquelle est monté le filtre Hα. Il s’agit d’un filtre Hα d’un diamètre de 36 mm de la marque Astronomik ayant une bande passante de 6 nm. Une courbe typique de transmission de ce filtre est donnée sur la figure 3.
• Un spectroscope Alpy 600 fabriqué par la société Shelyak. Il s’agit d’un grism, anglicisme désignant un instrument d’optique composé d’un réseau (ici à 600 traits/mm) et d’un prisme (grism = grating + prism). Le réseau permet de décomposer la lumière de la source car chaque rayonnement sort du réseau avec un angle qui dépend de sa longueur d’onde. L’Alpy 600 est également composé d’une fente (ici de 23 μm largeur), d’un collimateur pour rendre les rayons lumineux parallèles et d’un objectif pour focaliser le spectre sur le capteur du détecteur.
• Une caméra CCD Atik 4000 monochrome ayant un capteur de 2048×2048 pixel de 7,4 μm de côté.

L’extraction et le traitement des spectres ont été réalisé avec le logiciel ISIS développé par Christian Buil.

III. Mesure de la courbe de transmission

1. Etalonnage du système

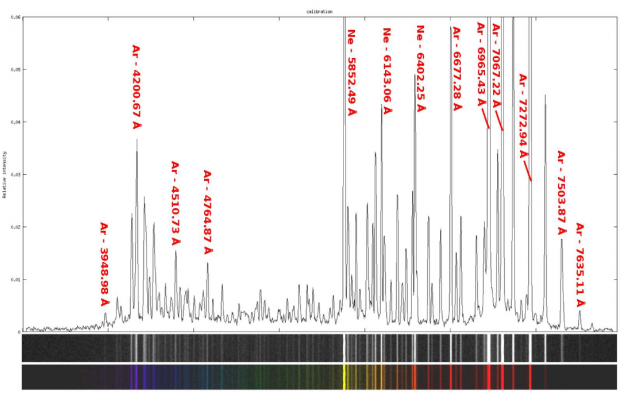
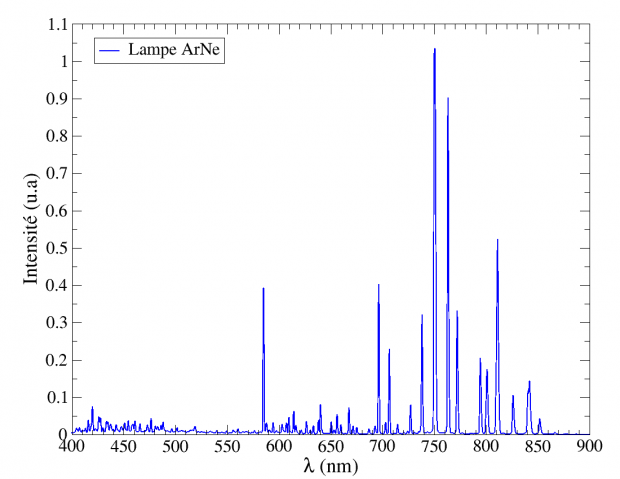
La première étape nécessaire à la mesure de la courbe de transmission est l’étalonnage du système spectroscope/CCD. Cette étape consiste à convertir l’axe en pixel des spectres en axe longueur d’onde. Pour cela, il faut utiliser une source lumineuse dont le spectre est parfaitement connu. Une telle source est appelée lampe d’étalonnage. Le module Alpy contient une lampe ArNe dont le spectre est donné sur la figure 4 (1 Å = 0,1 nm)

La figure 5 présente l’image de lampe ArNe obtenue avec la CCD. Le capteur étant monochrome, l’image a été colorisée a posteriori.

Les raies en émission sont clairement visibles sur cette image. La courbure est due à la configuration optique de l’Alpy 600 : il s’agit de l’effet de « smile ». A partir de cette image 2D, ISIS extrait le spectre 1D présenté sur la figure 6.

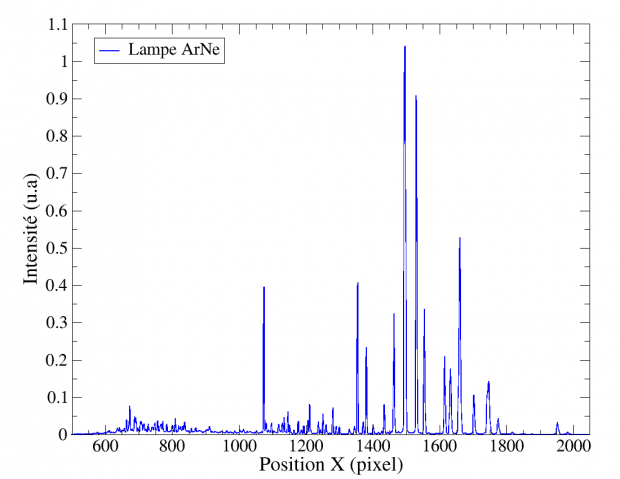
ISIS doit alors calculer une loi de dispersion de type polynomial : λ(X)= a₀ + a₁X +a₂X² + a₃X³ a₄X⁴ où X est la position sur le spectre en pixel et a_i sont des paramètres calculés pour reproduire les rais étalons. Pour cela, les centres de plusieurs raies du spectre non étalonné de la lampe ArNe sont mesurés. Comme les longueurs d’onde de ces raies sont connues (voir figure 4), la conversion pixel – longueur d’onde est déterminée pour toutes ces raies et les coefficients a_i sont déduits. A l’issue de la phase d’étalonnage, nous obtenons le spectre présenté sur la figure 7. Nous venons donc de convertir l’axe des abscisses du spectre de « pixel » à « longueur d’onde », qui est une quantité physique exploitable. Notre spectroscope est désormais étalonné en longueur d’onde. Nous pouvons nous consacrer à la mesure de la courbe de transmission du filtre Hα.

2. Procédure de mesure de la transmission du filtre

Deux spectres sont nécessaires afin d’obtenir la courbe de transmission du filtre Hα. Le spectre d’une lumière blanche uniforme (lampe de flat) avec et sans filtre Hα entre la lampe et le spectroscope. Notons I^CCD(λ) l’intensité lumineuse d’un pixel correspondant à une longueur d’onde λ sur l’image obtenue avec la CCD. Sans filtre Hα, I^{CCD sans filtre} (λ) est donné par : I^{CCD sans filtre} (λ) = I^source(λ).R^CCD/Alpy(λ) où R^CCD/Alpy(λ) est la réponse du système spectroscope/capteur CCD à la longueur d’onde λ. Avec l’ajout du filtre Hα, I^CCD(λ) devient : I^{CCD avec filtre}(λ) = I^source(λ).R^CCD/Alpy(λ).T^filtre(λ) où T^filtre(λ) est la transmission du filtre à la longueur d’onde λ. Si l’on suppose que l’intensité de la source et la réponse du système spectroscope/CCD n’ont pas variées entre les deux mesures, la transmission du filtre à la longueur d’onde l est donné par : T^filtre(λ) = I^{CCD avec filtre}(λ)/I^{CCD sans filtre} (λ). Ainsi la courbe de transmission du filtre est donnée par le rapport entre le spectre de la lampe de flat mesuré avec filtre et sans filtre.

3. Spectres de la lampe de flat avec et sans filtre Hα

La figure 8 présente les spectres obtenus avec la lampe de flat avec et sans filtre Hα. 15 poses de 10 s ont été additionnées pour obtenir ces spectres. Les images maître d’offset et de dark ont été préalablement retirées aux images brutes.

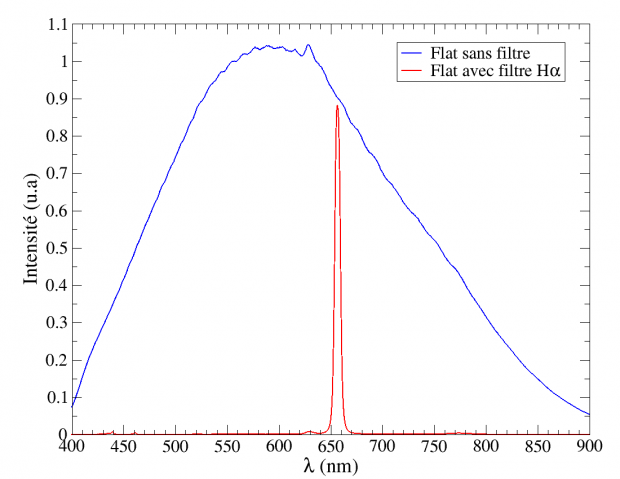
L’effet du filtre Hα est nettement visible puisque seule une très faible partie du spectre de la lampe de flat (en bleu) est transmise au capteur CCD par le spectroscope. La forme du spectre de la lampe de flat (en bleu) est due à la réponse du capteur CCD qui n’est pas constante dans le visible.

4. Courbe de transmission

Afin d’obtenir la courbe de transmission le spectre avec filtre (en rouge) est divisé par le spectre obtenu sans ce même filtre (en bleu). Le résultat est donné sur la figure 9.

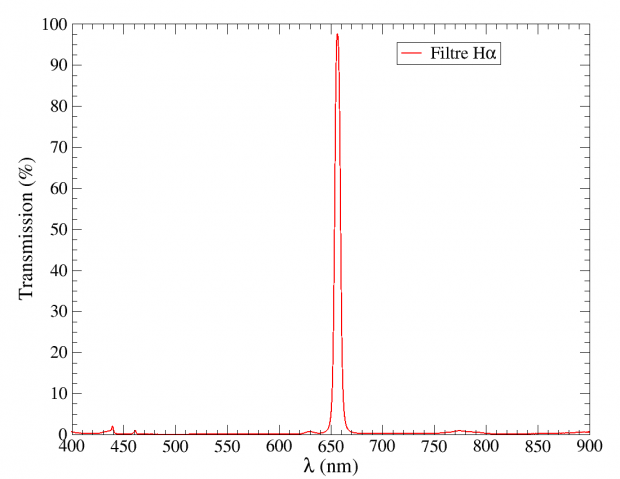
Un zoom de cette courbe autour de la raie Hα est présenté sur la figure 10.

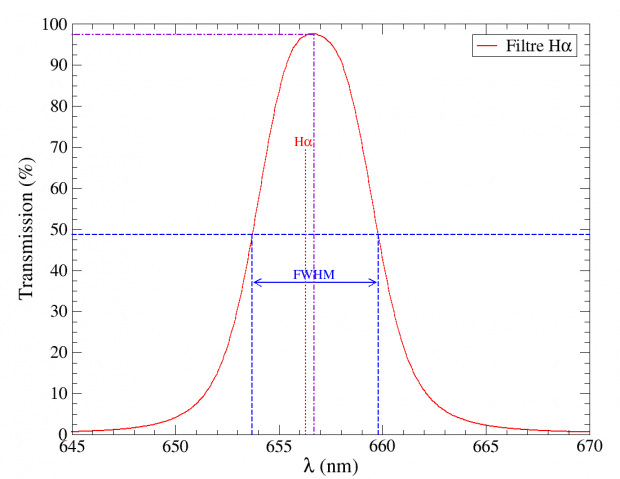
Sur ce zoom, nous constatons que la transmission maximale du filtre est excellente : 97,4% à 656,7 nm. La largeur à mi-hauteur (FWHM) de la courbe de transmission du filtre est de 6,1 nm, ce qui est en accord avec les données du constructeur. Notons cependant, que la longueur d’onde centrale de la bande passante du filtre est légèrement décalée par rapport à la raie Hα (656,3 nm). La courbe de transmission obtenue est donc parfaitement en accord avec celle du constructeur (figure 3).

Conclusion

Dans cet article, nous avons utilisé un spectroscope pour mesurer la courbe de transmission d’un filtre Hα. Celle-ci est une caractéristique essentielle du filtre qui est généralement fournie par le constructeur. Nous venons de mettre en évidence une méthode simple pour vérifier ces données.